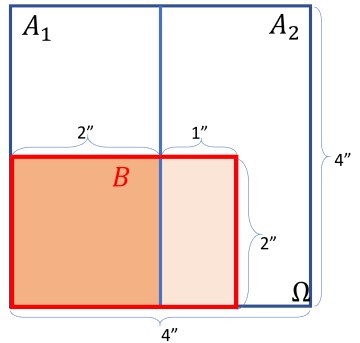
We observe that ${A_1,A_2}$ is a partition of $\Omega$. Applying the law of total probability to this partition,

$$P(B) = P(A_1)P(B|A_1) + P(A_2)P(B|A_2)$$

Notice that rectangles $A_1$ and $A_2$ have the same area, so $P(A_1) = P(A_2) = 1/2$. Rectangle $B \cap A_1$ has half the height of rectangle $A_1$ and the same width, so $P(B|A_1) = P(B \cap A_1) / P(A_1) = 1/2$. Rectangle $B \cap A_2$ has half the height and half the width of rectangle $A_2$, so $P(B|A_2) = P(B \cap A_2) / P(A_2) = 1/4$. Plugging these numbers into the law of total probability above,

$$P(B) = (1/2)(1/2) + (1/2)(1/4) = 3/8$$