3.5 Computing Examples

3.5.1 Expected Value of Education [discrete random variable]

• The expected value of a discrete random variable \(X\) is the weighted average of the values in the range of \(X\).
• Suppose that \(X\) represents the number of years of education that someone has completed, and so has a support that ranges from \(0\) years of education, up to \(28\) years of education. (Incidentally, Mark Labovitz has about 28 years of education.)
• You can then think of

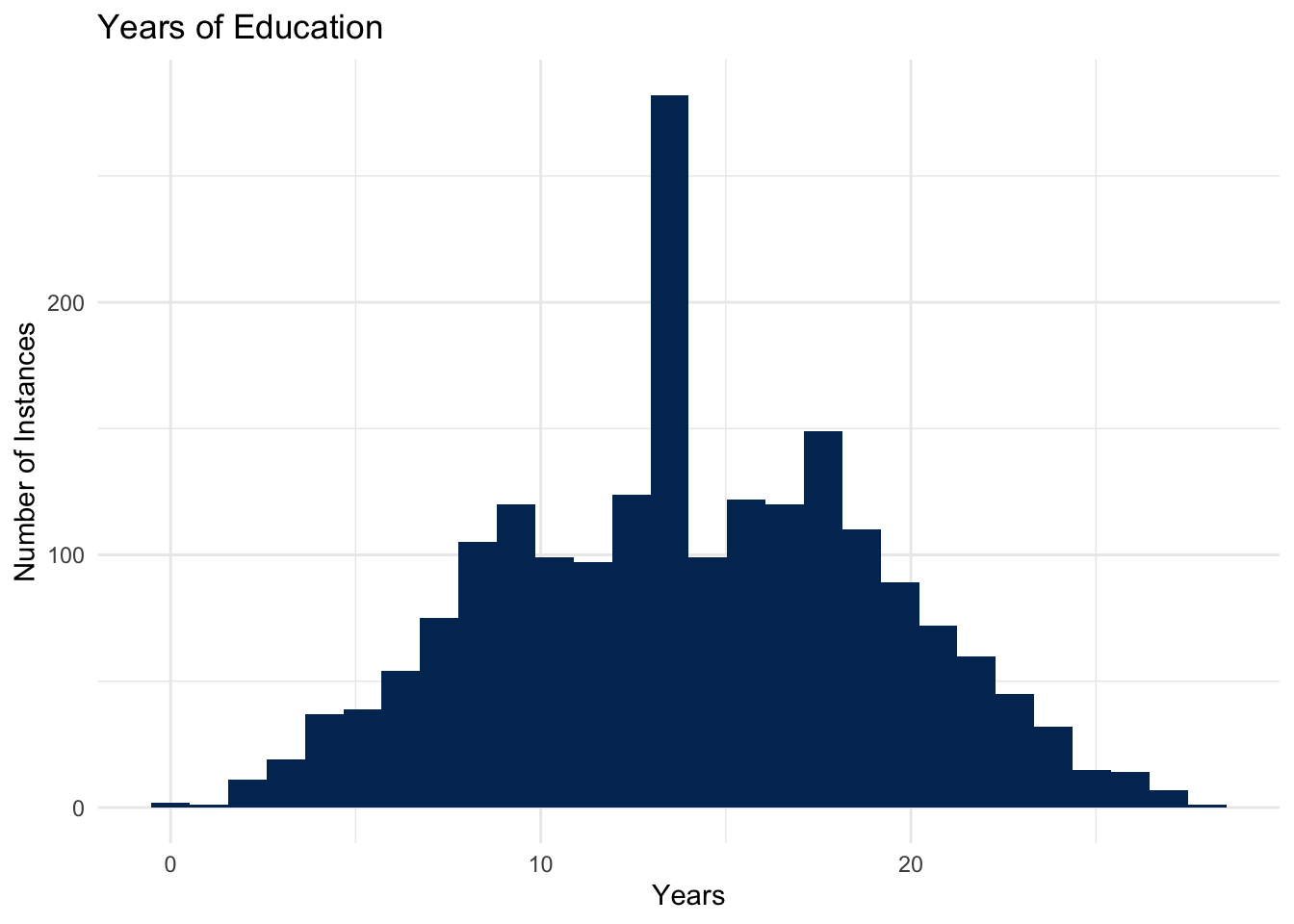
• Without using specific numbers, describe the process you would use to calculate the expected value of this distribution.

3.5.2 Using a formula

• Does the following formula match with your intuitive description of the expected value? Why, or why not?

\[ \begin{aligned} E[X] &= \sum_{x \in \{EDU\}} x \cdot f(x) \\ &= \sum_{x=0}^{x=28} x\cdot P(X=x) \end{aligned} \]