7.11

7.11.1 The Poisson Distribution

The poisson distribution has the following PDF:

\[ f_X(x) = \frac{\lambda^n e^{-\lambda}}{n!} \]

The key shape parameter for a poisson function is \(\lambda\); we show three different distributions, setting this shape parameter to be 1, 3, and 30 respectively. Notice that the limits on these plots are not set to be the same; for example, the range in the third plot is considerably larger than the first.

Code

pois_lambda_1  <- rpois(n=1000, lambda=1)
pois_lambda_3  <- rpois(n=1000, lambda=3)
pois_lambda_30 <- rpois(n=1000, lambda=30)

plot_1  <- ggplot() + aes(x=pois_lambda_1) + geom_histogram(bins=6, fill = berkeley_blue)
plot_3  <- ggplot() + aes(x=pois_lambda_3) + geom_histogram(bins=10, fill = berkeley_gold)
plot_30 <- ggplot() + aes(x=pois_lambda_30) + geom_histogram(bins=30, fill = berkeley_sather)

plot_1 / plot_3 / plot_30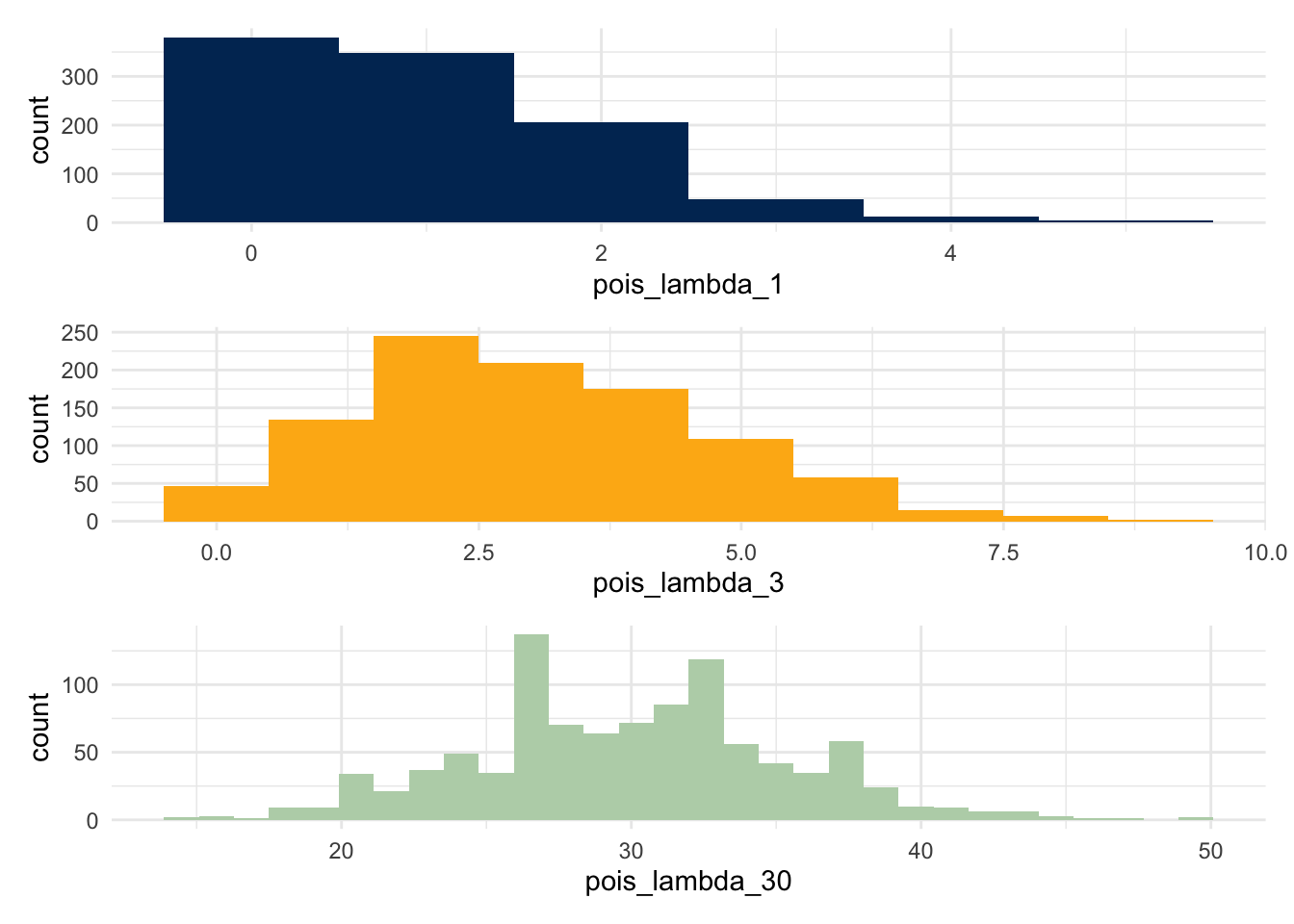

What does this changing distribution do to the p-values?

7.11.2 Write a Simulation

Code

pois_sim <- function(num_observations, lambda_one, lambda_two) { 
  
  t_test_result <- rep(NA, 10000)
  wilcox_result <- rep(NA, 10000)
  
  for(i in 1:10000) { 
    group_one <- rpois(n=num_observations, lambda=lambda_one)
    group_two <- rpois(n=num_observations, lambda=lambda_two)
  
    t_test_result[i] <- t.test(group_one, group_two)$p.value
    wilcox_result[i] <- wilcox.test(x=group_one, y=group_two)$p.value
  }
  
  df <- data.table(
    p_value = c(t_test_result, wilcox_result), 
    test    = rep(c('t_test', 'wilcox_test'), each = 10000)
  )
  
  return(df)
}

Code

foo <- pois_sim(20, 1, 2.0)

Code

foo %>%
  ggplot() +
  geom_density(aes(x=p_value, color = test)) +
  scale_color_manual(values = c(berkeley_blue, berkeley_gold))

And so, the simulation rejects the null at the following rates:

For the t-test, at a rate of 0.0650033
For the Wilcox test, at a rate of 0.0748107

7.11.3 What if a distribution is much more skewed?

Code

skewed_sim <- function(num_sims=1000, num_observations, alpha_1, beta_1, alpha_2, beta_2) {
  
  t_test_result <- rep(NA, num_sims)
  wilcox_result <- rep(NA, num_sims)
  
  for(i in 1:num_sims) { 
    group_one <- rbeta(n=num_observations, shape1 = alpha_1, shape2 = beta_1)
    group_two <- rbeta(n=num_observations, shape1 = alpha_2, shape2 = beta_2)
  
    t_test_result[i] <- t.test(group_one, group_two)$p.value
    wilcox_result[i] <- wilcox.test(x=group_one, y=group_two)$p.value
  }
  
  dt <- data.table(
    p_value = c(t_test_result, wilcox_result), 
    test    = rep(c('t_test', 'wilcox_test'), each = num_sims)
  )
  
  return(dt)
}

7.11.4 False Rejection Rates

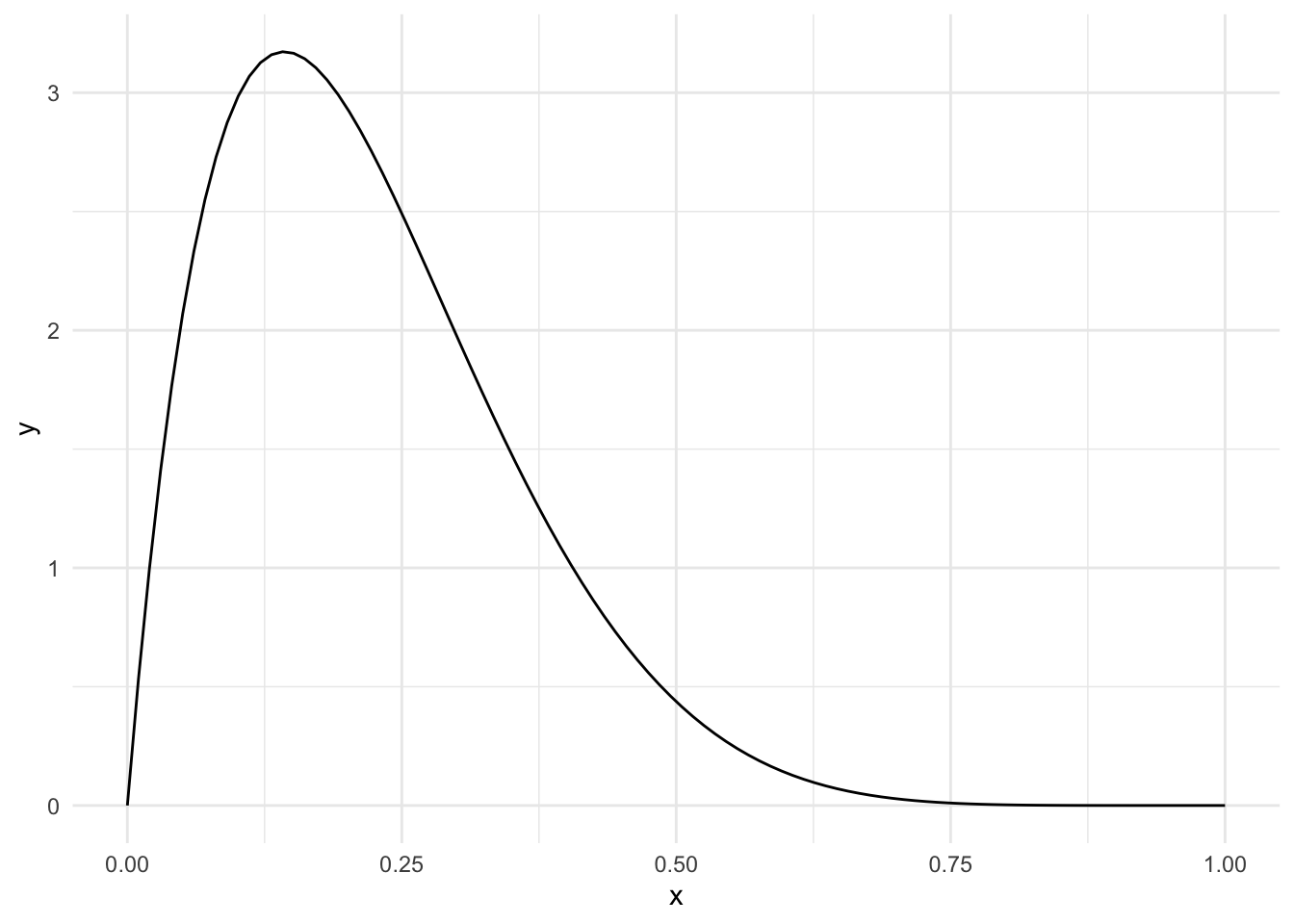
Start with a distribution that has parameters alpha=2, beta=7.

Code

ggplot(data.frame(x=c(0,1)), aes(x)) + 
  stat_function(fun = dbeta, n=100, args=list(shape1=2, shape2=7))

Code

same_dist_small_data <- skewed_sim(
  num_observations=10, 
  alpha_1=2, beta_1=7, 
  alpha_2=2, beta_2=7
  )
same_dist_med_data <- skewed_sim(
  num_observations=50, 
  alpha_1=2, beta_1=7, 
  alpha_2=2, beta_2=7
  )
same_dist_big_data <- skewed_sim( # haha, "big data"
  num_observations=100, 
  alpha_1=2, beta_1=7, 
  alpha_2=2, beta_2=7
  )

Code

plot_1 <- same_dist_small_data %>%
  ggplot() +
  geom_density(aes(x=p_value, color = test), bounds=c(0,1)) +
  scale_color_manual(values = c(berkeley_blue, berkeley_gold))
plot_2 <- same_dist_med_data %>%
  ggplot() +
  geom_density(aes(x=p_value, color = test), bounds=c(0,1)) +
  scale_color_manual(values = c(berkeley_blue, berkeley_gold))
plot_3 <- same_dist_big_data %>%
  ggplot() +
  geom_density(aes(x=p_value, color = test), bounds=c(0,1)) +
  scale_color_manual(values = c(berkeley_blue, berkeley_gold))

plot_1 / plot_2 / plot_3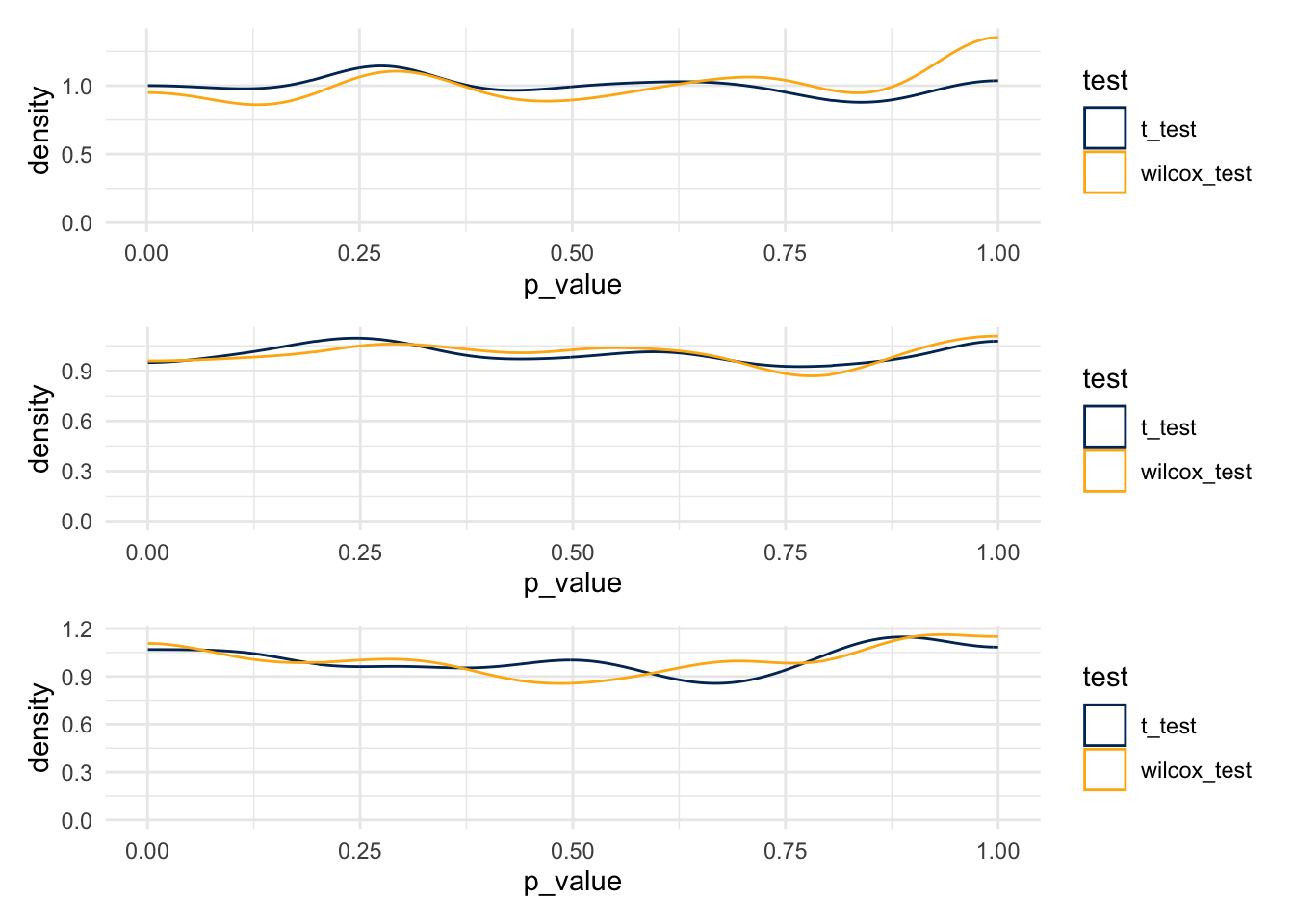

T-tests
- 0.055
- 0.046
- 0.056
Wilcox Tests
- 0.046
- 0.048
- 0.061

7.11.5 What about Power to Reject

Code

small_diff_small_data <- skewed_sim(
  num_observations=10, 
  alpha_1=2, beta_1=7, 
  alpha_2=2, beta_2=5
  )
small_diff_med_data <- skewed_sim(
  num_observations=50, 
  alpha_1=2, beta_1=7, 
  alpha_2=2, beta_2=5
  )
small_diff_big_data <- skewed_sim( # haha, "big data"
  num_observations=100, 
  alpha_1=2, beta_1=7, 
  alpha_2=2, beta_2=5
  )

Code

plot_1 <- small_diff_small_data %>%
  ggplot() +
  geom_density(aes(x=p_value, color = test), bounds=c(0,1)) +
  scale_color_manual(values = c(berkeley_blue, berkeley_gold))
plot_2 <- small_diff_med_data %>%
  ggplot() +
  geom_density(aes(x=p_value, color = test), bounds=c(0,1)) +
  scale_color_manual(values = c(berkeley_blue, berkeley_gold))
plot_3 <- small_diff_big_data %>%
  ggplot() +
  geom_density(aes(x=p_value, color = test), bounds=c(0,1)) +
  scale_color_manual(values = c(berkeley_blue, berkeley_gold))

plot_1 / plot_2 / plot_3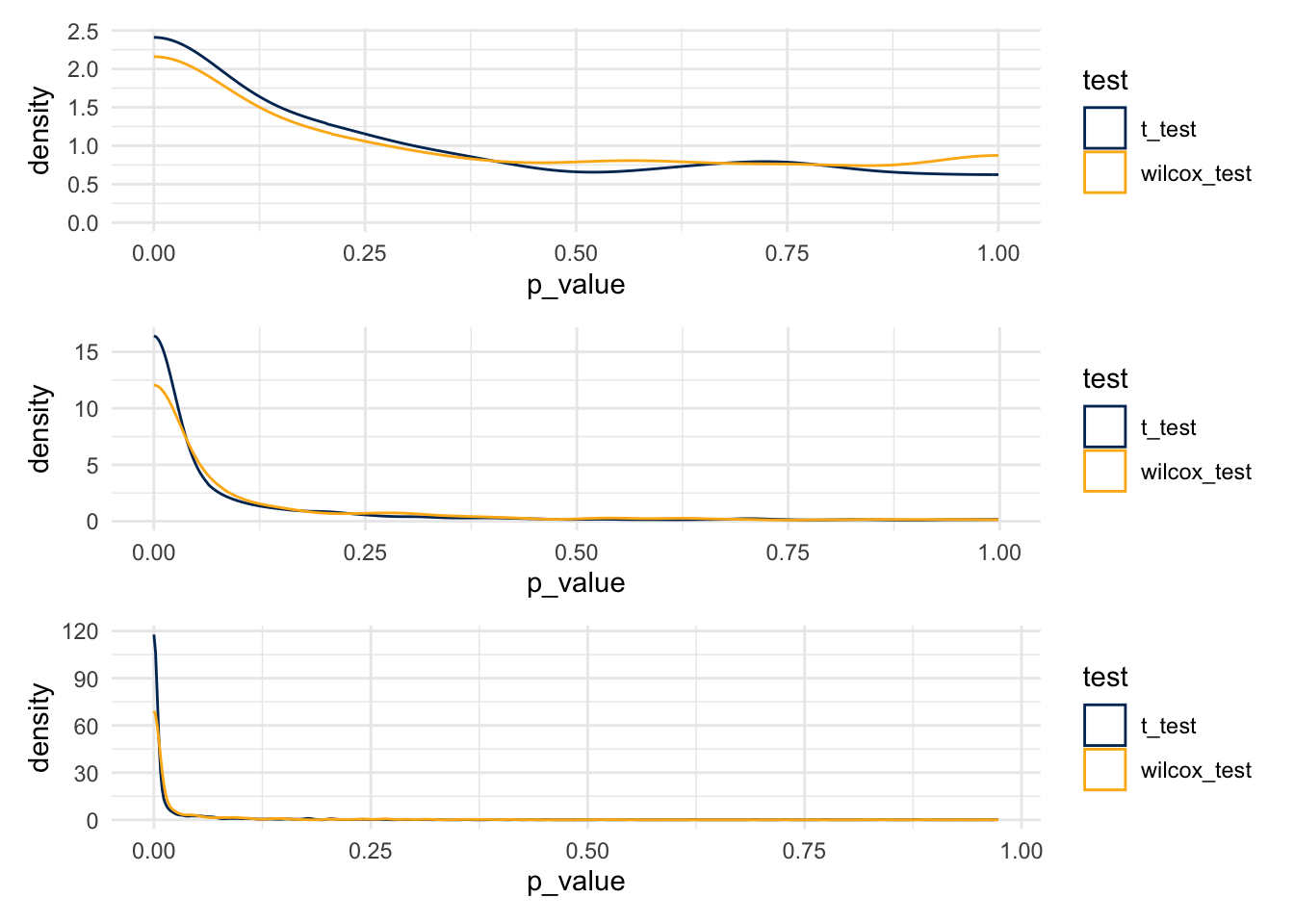

7.11.6 Paired compared to unpaired tests

Code

paired_sim <- function(num_sims=10000, num_observations, mean_one, mean_two, paired_diff, sd_one, sd_two) { 
  
  unpaired_test_unpaired_data <- rep(NA, num_sims)
  unpaired_test_paired_data   <- rep(NA, num_sims)
  paired_test_unpaired_data   <- rep(NA, num_sims)
  paired_test_paired_data     <- rep(NA, num_sims)
  
  for(i in 1:num_sims) { 
    observation_a1 <- rnorm(n = num_observations, mean = mean_one, sd = sd_one) 
    ## first create unpaired data 
    observation_b <- rnorm(n = num_observations, mean = mean_two, sd = sd_two)
    ## then, create paired data 
    observation_a2 <- observation_a1 + rnorm(n = num_observations, mean = paired_diff, sd=sd_two)
    
    ## run tests
    unpaired_test_unpaired_data[i] <- t.test(x=observation_a1, y=observation_b,  paired=FALSE)$p.value
    unpaired_test_paired_data[i]   <- t.test(x=observation_a1, y=observation_a2,  paired=FALSE)$p.value
    paired_test_unpaired_data[i]   <- t.test(x=observation_a1, y=observation_b,  paired=TRUE)$p.value
    paired_test_paired_data[i]     <- t.test(x=observation_a1, y=observation_a2, paired=TRUE)$p.value
  }
  
  dt <- data.table(
    p_value = c(unpaired_test_unpaired_data, unpaired_test_paired_data, 
                paired_test_unpaired_data,   paired_test_paired_data), 
    test    = rep(c('unpaired data, unpaired test', 'paired data, unpaired test', 
                    'unpaired data, paired test', 'paired data, paired test'), each = num_sims)
  )
  
  return(dt)
}

Code

bar <- paired_sim(num_observations = 30,  mean_one = 10, mean_two = 11, paired_diff = 1, sd_one = 4, sd_two = 5)

Code

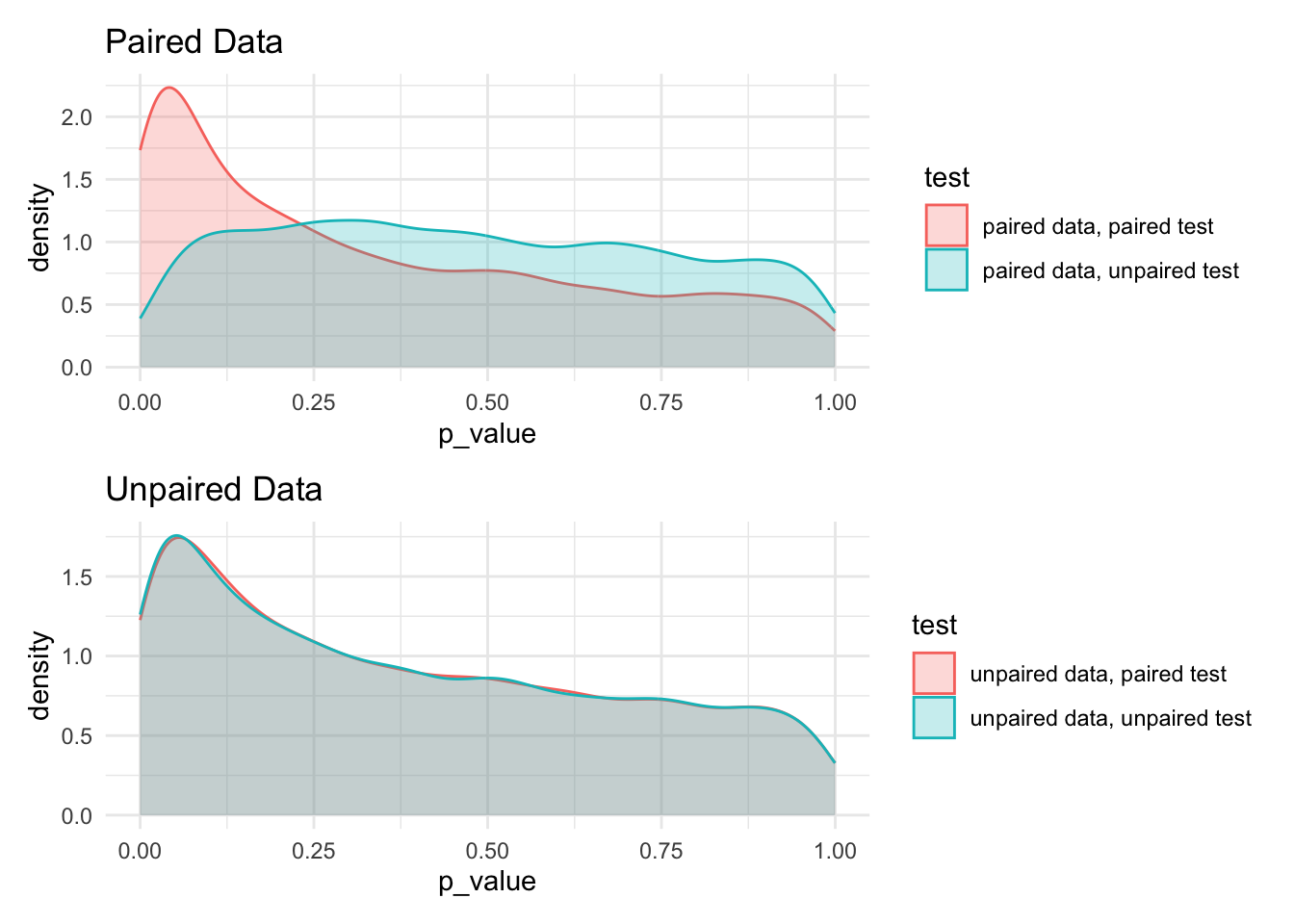
paired_data_plot <- bar[grep('unpaired data', test, invert=TRUE)] %>% 
  ggplot() + 
    aes(x=p_value, color = test, fill = test) + 
    geom_density(alpha=0.25) + 
  labs(title = 'Paired Data')
unpaired_data_plot <- bar[grep('unpaired data', test, invert=FALSE)] %>% 
  ggplot() + 
    aes(x=p_value, color = test, fill = test) + 
    geom_density(alpha=0.25) + 
  labs(title = 'Unpaired Data')

paired_data_plot / unpaired_data_plot