6.9 Falling Ill (The General Form of a Hypothesis Test)

In the async content for the week, we’re really, really clear that we’re only working with the t-distribution. But, the general “form” of a frequentist hypothesis test is always the same: produce a test statistic; produce a distribution of that test statistic if the null hypothesis were true; then compare the two. Let’s stretch this application a little bit.

There is a theory that upcoming tests cause students to fall ill. We have been collecting wellness data from our students for several years (not really…) and we have found the following distribution of illnesses (Notice that this does not tell you anything about how many students we have enrolled over the years):

• 20 students have reported being ill in the week before Test 2

• 10 students have reported being ill in the week after Test 2

Think of wellness/illness as a dichotomous statement.

• State an appropriate null hypothesis. After you have stated this null hypothesis, can you think about (or, even better) can you produce a distribution of the probability of {0, 1, 2, 3, … 30} of the illnesses reported before the test?

Code

null_distribution <- dbinom(0:30, 30, prob = 0.5)

ggplot() + 
  aes(x=0:30, y=null_distribution) + 
  geom_col()

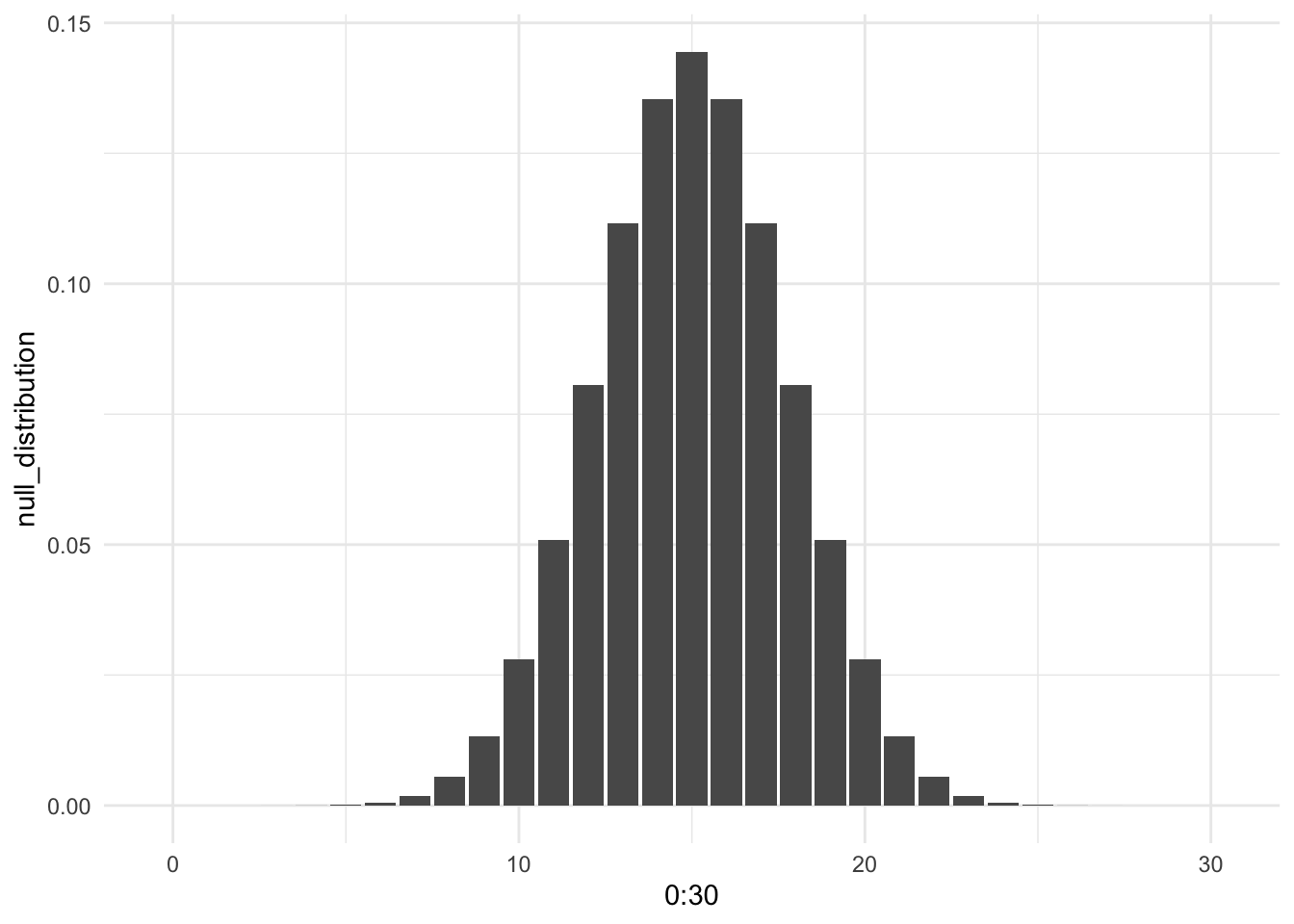
• State a rejection criteria. What occurrence in the data would cause you do doubt the plausibility of your null hypothesis?

• What do you conclude? Given the data that is presented to you and the null hypothesis, what do you conclude?