6.10 Data Exercise

t-Test Micro Cheat Sheet

In order for a t-test to produce valid results, a set of conditions must be satisfied. While the literature refers to these as assumptions, you might do better to refer to these for yourselves as requirements. Meaning, if these requirements for the data generating process are not satisfied, the test does not produce results that hold any statistical guarantees.

Metric variable: The data needs to be numeric
IID: The data needs to be sampled using an independent, identically distributed sampling process.
Well-behaved: The data need to demonstate no major deviations from normality, considering sample size

Testing the Home Team Advantage

The file ./data/home_team.csv contains data on college football games. The data is provided by Wooldridge and was collected by Paul Anderson, an MSU economics major, for a term project. Football records and scores are from 1993 football season.

Code

home_team <- read.csv('./data/home_team.csv') %>% 
  select(dscore, dinstt, doutstt) %>% 
  rename(
    score_diff               = dscore, 
    in_state_tuition_diff    = dinstt, 
    out_state_tuition_diff   = doutstt
  )

glimpse(home_team, width = 80)

## Rows: 30
## Columns: 3
## $ score_diff             <int> 10, -14, 23, 8, -12, 7, -21, -5, -3, -32, 9, 1,…
## $ in_state_tuition_diff  <int> -409, NA, -654, -222, -10, 494, 2, 96, 223, -20…
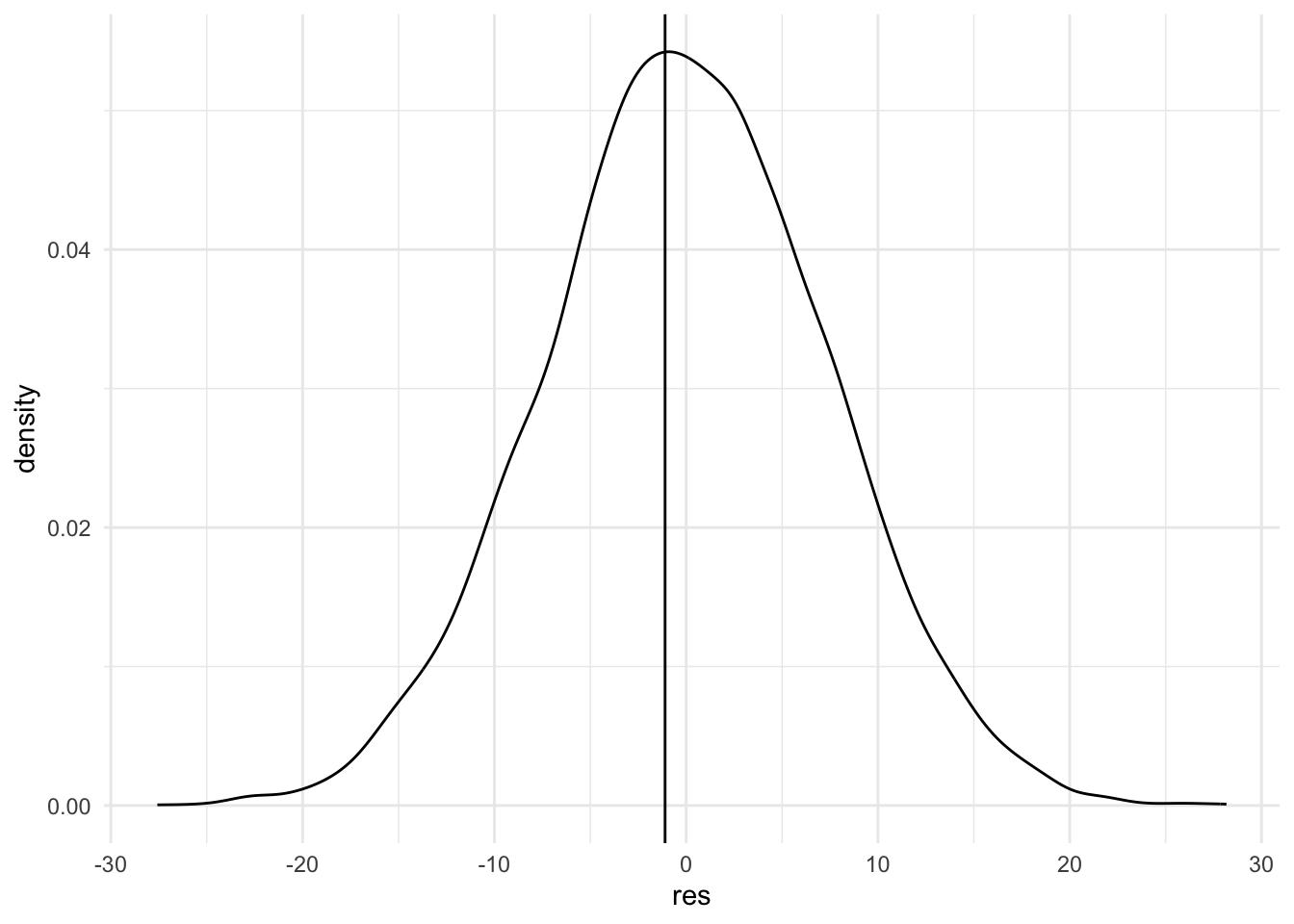
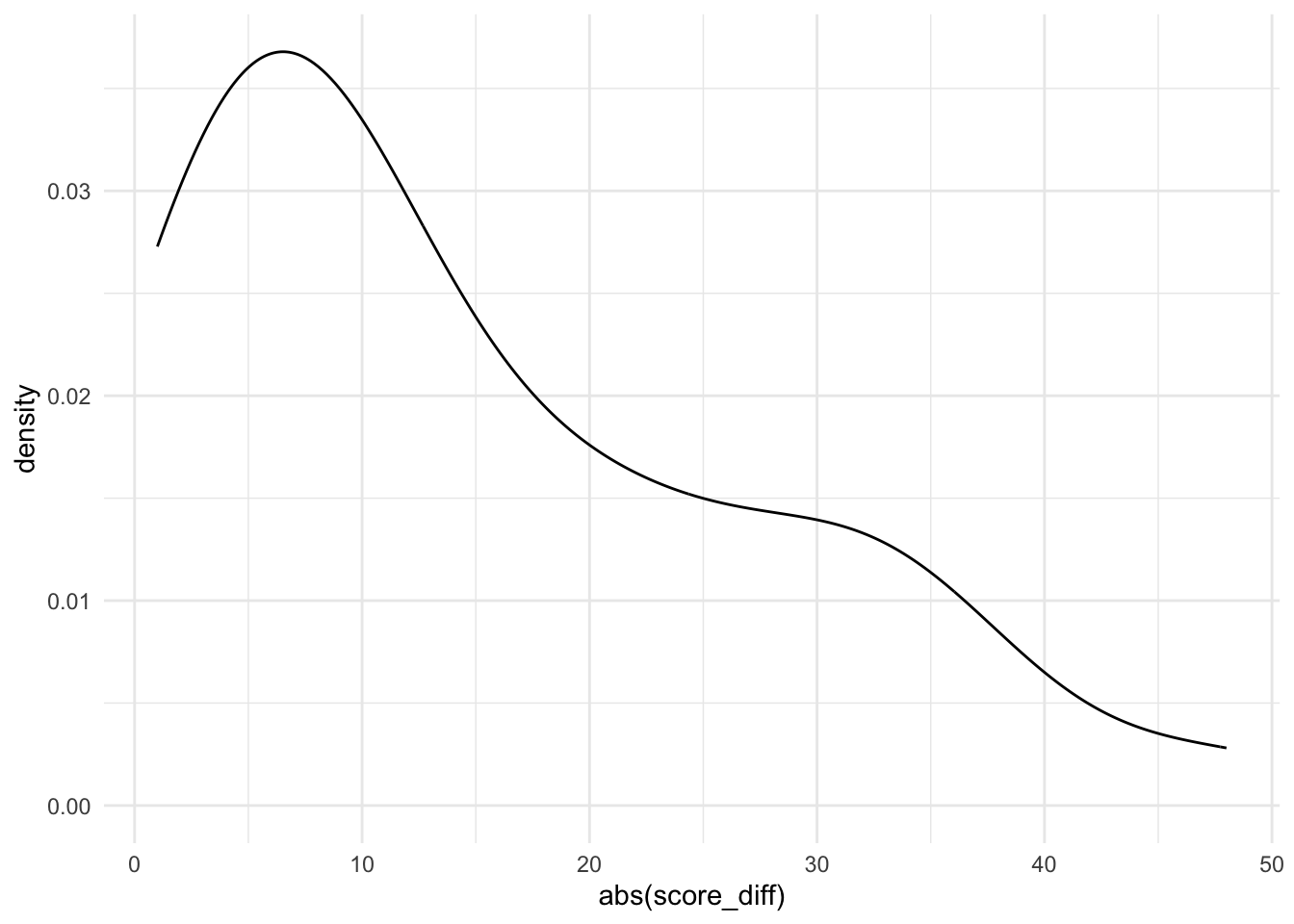
## $ out_state_tuition_diff <int> -4679, -66, -637, 456, 208, 17, 2, -333, 2526, …

We are especially interested in the variable, score_diff, which represents the score differential, home team score - visiting team score. We would like to test whether a home team really has an advantage over the visiting team.

The instructor will assign you to one of two teams. Team 1 will argue that the t-test is appropriate to this scenario. Team 2 will argue that the t-test is invalid. Take a few minutes to examine the data, then formulate your best argument.
Should you perform a one-tailed test or a two-tailed test? What is the strongest argument for your answer?

Code

## I'm going two-tailed. 
## H0 : No effect of being home or away
## HA : There IS some effect.

Execute the t-test and interpret every component of the output.

Code

t.test(x=home_team$score_diff, mu=0, alternative = 'two.sided')

## 
##  One Sample t-test
## 
## data:  home_team$score_diff
## t = -0.30781, df = 29, p-value = 0.7604
## alternative hypothesis: true mean is not equal to 0
## 95 percent confidence interval:
##  -8.408919  6.208919
## sample estimates:
## mean of x 
##      -1.1

Code

res <- NA
for(i in 1:10000) {
  res[i] <- mean(rnorm(n=7, sd=sd(home_team$score_diff)))
}

ggplot() + 
  aes(x=res) + 
  geom_density() + 
  geom_vline(xintercept=mean(home_team$score_diff))

Code

home_team %>% 
  ggplot() + 
  aes(x=abs(score_diff)) + 
  geom_density()

Code

mean(home_team$score_diff)

## [1] -1.1

Code

mean((res < mean(home_team$score_diff))) + mean(res > abs(mean(home_team$score_diff)))

## [1] 0.881

Based on your output, suggest a different hypothesis that would have led to a different test result. Try executing the test to confirm that you are correct.